How Far Can You See at Sea?

Let’s say you’re standing on the beach, staring out across a perfectly flat ocean, wondering how far you can see before the planet curves out of view. A boat disappears into the distance, and someone next to you says, "It's over the horizon."

But what is the horizon, really? How far away is it? And how much farther could you see if you were taller, on a mountain, or just had really, really long legs?

Let’s dig in.

Chapter 1: Your Eyes vs. The Planet

Let’s start simple. You’re two meters tall, standing barefoot at sea level. How far is the horizon?

Quick answer: About 5.05 kilometers (3.14 miles).

Why that number? Because Earth is round (sorry, flat-Earthers) and geometry is a thing. The curvature of Earth means there's a certain point where the surface literally falls away from your line of sight. That point is your personal horizon.

Here’s the pocket formula for the distance to the horizon ^{[1] [2] [3]}:

d ≈ 3.57 √h (in km, with h in meters)

So if you plug in your 2 meters:

d ≈ 3.57 √2 ≈ 5.05 km

Boom. There’s your horizon.

Chapter 2: The World Bends (Slightly)

That 5.05 km assumes that light travels in a straight line. But light, like a teenager trying to get out of chores, doesn't always behave that way. Thanks to something called atmospheric refraction, light bends ever so slightly downward as it passes through layers of air that get thinner with altitude.

This makes Earth look a bit flatter than it is. So we fudge the math a little by pretending the Earth is about 1/6 larger ^[1:1]:

d ≈ 3.86 √h

That means your 5.05 km suddenly stretches to around 5.45 km.

Congratulations, you can now see 400 extra meters, thanks to air!

But don’t get too excited. This bending varies with weather. On some days, you might see less. On rare days, way more — hello, mirages! ^[4]

Chapter 3: Height is Might

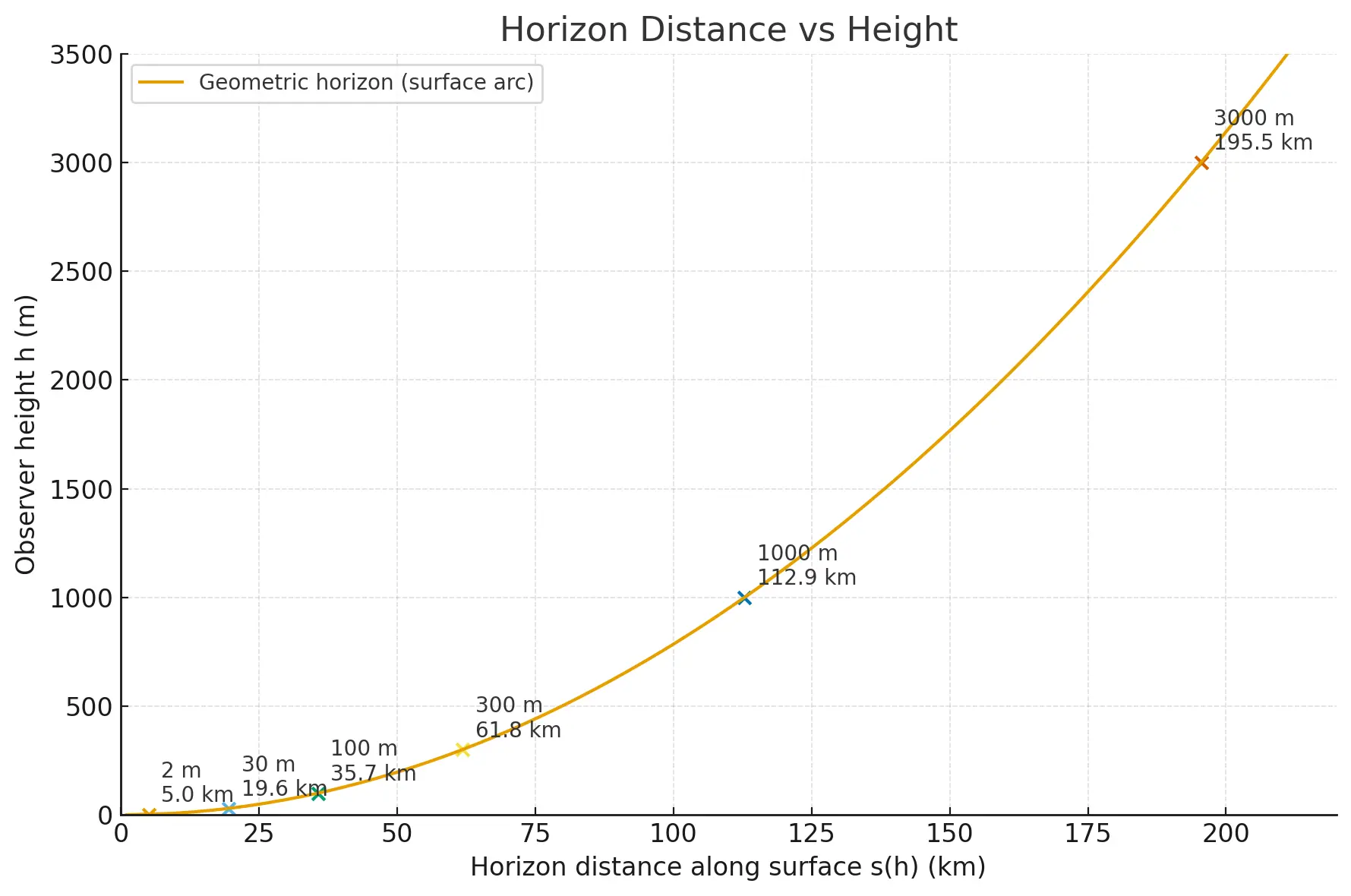
Let’s play the "What If I Were Taller?" game. How does increasing your height increase your visible range?

Spoiler: not as much as you'd think.

Your distance to the horizon grows with the square root of your height. So to double your viewing range, you have to be four times taller ^{[1:2] [2:1]}.

Examples:

• 2 meters: 5.05 km
• 8 meters (a really big giraffe?): 10.1 km
• 100 meters (top of a skyscraper): 35.7 km
• 10,000 meters (cruising in a jet): 356.7 km
• 400,000 meters (International Space Station): 2,201 km

Still not the whole planet though. So... is there a maximum?

Yup.

Because Earth is a sphere, the absolute furthest you could ever see along its surface (from any one point) is one quarter of its circumference — about 10,007 km ^{[3:1] [5]}.

You’d have to be floating in space to get close to that.

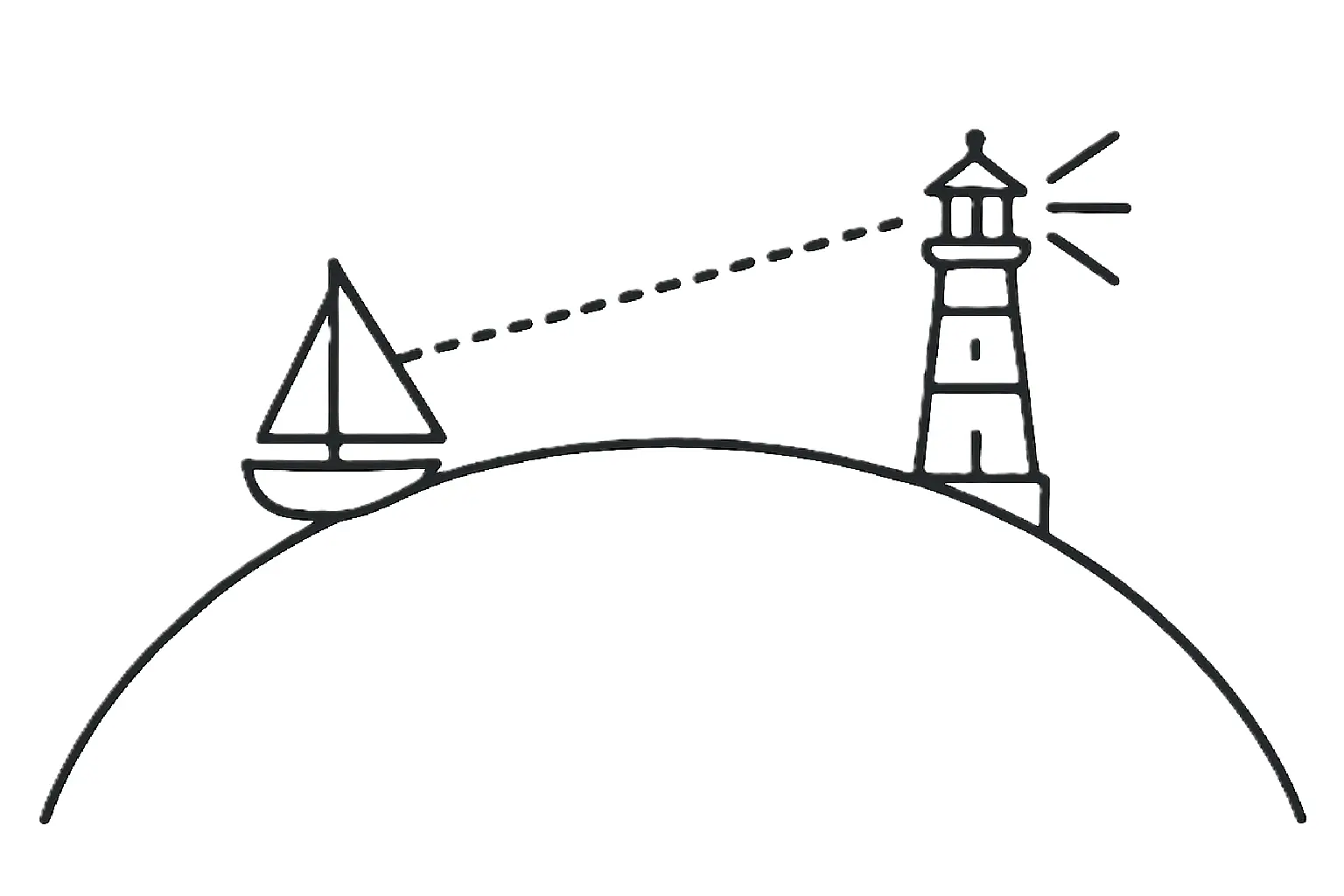
Chapter 4: Two Viewers Are Better Than One

Now, imagine you’re on a boat and trying to spot a lighthouse. Both of you are above sea level. Your eyes are 2 m up, and the lighthouse is 30 m tall. Can you see it?

Add your two horizon distances together:

• You: 5.05 km
• Lighthouse: 19.6 km

Total: 24.65 km — that’s how far away it can be and still peek over your horizon.

With typical refraction? You might get 26.6 km. This “add-your-horizons” trick is how mariners calculate geographic range ^[6].

Chapter 5: The Flat Earth Thought Experiment

Okay, okay. What if the Earth really were flat? How far could you see then?

Answer: As far as the air lets you.

In a world without curvature, there's no geometric horizon. But visibility would still be limited by dust, haze, fog, and the usual suspects. Under perfect conditions, you might see 100+ km. In a city? Maybe 5 km. The science behind this uses Koschmieder's law, which links visibility to how much light is scattered by particles in the air ^[7].

Bonus fun: atmospheric bending can occasionally produce looming or superior mirages, where you see objects beyond the horizon thanks to weird thermal layers. Like nature's own cheat code ^[4:1].

Chapter 6: The Exact Math (For Nerds Only)

If you really want to impress people at parties, here are the exact formulas ^{[2:2] [1:3]}:

Line of sight distance:
ℓ(h) = √((R + h)² − R²) = √(h(2R + h))

Surface distance (arc length):
s(h) = R · arccos(R/(R + h))

For most casual purposes, the trusty
d ≈ 3.57 √h
gets you close enough.

Just don’t forget the units. And maybe wear sunscreen.

Final Thoughts: More Height, More Horizon, But...

We live on a giant sphere, wrapped in a fuzzy shell of atmosphere, trying to see just a little farther.

Your height gives you power, but only in square-rooty little chunks. The air helps a bit, unless it doesn't. And in the end, unless you're on the ISS or beyond, you're only ever going to see a small slice of this big blue ball.

But hey — it's a beautiful slice.

Sources